0152.一道非典型动态规划题

Leetcode动态规划的题目152. Maximum Product Subarray

题目不难，是53. Maximum Subarray的拓展。

标准的解法就是动态规划，时间复杂度O(n)，空间复杂度O(1)。《算法导论》为了介绍分治，在第四章Divide-and-Conquer，介绍了另一种方法，时间复杂度为O(nlogn)，此处不再赘述。

lee215大牛的另一种解法令人耳目一新:

def maxProduct(self, A):
    B = A[::-1]
    for i in range(1, len(A)):
        A[i] *= A[i - 1] or 1
        B[i] *= B[i - 1] or 1
    return max(A + B)

首先，用0把数组划分为若干个子数组，最终的结果在0和不含0子数组中产生。

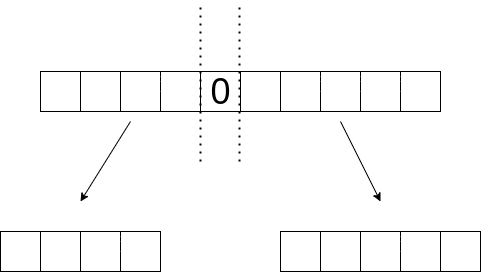
以一个不含0的长度为n的整数数组nums为例，最终可以证明，该数组的最大乘积，一定是从某端点出发，延展到某个位置为止。

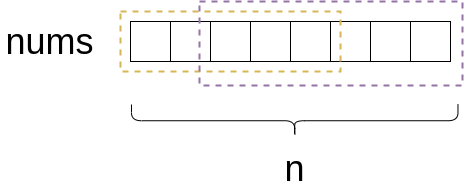
分类讨论

1. 假如这个数组没有负数，最大乘积一定是从最左端到最右端，结论成立
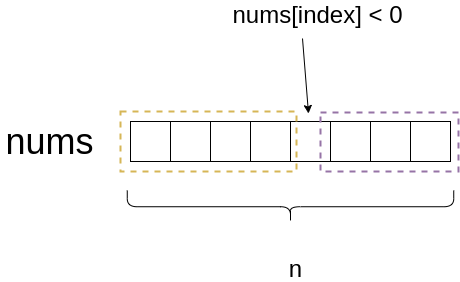
2. 假设这个数组包含1个负数，负数位于index，那最大乘积一定是由nums[0:index+1]或者nums[index:n]产生，结论成立

1. 假如这个数组包含偶数个负数，最大乘积一定是从最左端到最右端，结论成立
2. 假如这个数组包含3个负数，分割点一定是第一个负数(i)或者第三个负数(k)，结论成立

依此类推，这个结论是成立的。